大学への数学-再び-
ここまでで一区切りついたので、これまでのまとめをしたいと思います。いくつか説明が漏れているところもありまし、ここまでのの話が、この後どのように一般化されたのかについても説明できると思います。
\(x^{n}-1\)の因数分解
このシリーズは大学への数学に掲載されていた問題
\[x^{n}-1\ {\text を因数分解せよ}\]
から始まりました。
高校生だった私は、その当時全く気がつきませんでしたが、\(x^{n}-1\)の因数分解と自然数\(n\)の約数との間には深い関係があります。
\(x^{n}-1\)の因数分解と\(n\)の約数を表にしてみます。
| \(n\) | \(x^{n}-1\)の因数分解 | 因子の個数 | \(n\)の約数 | \(n\)の約数の個数 | |
|---|---|---|---|---|---|
| 2 | \((x-1)(x+1)\) | 2 | 1,2 | 2 | |
| 3 | \((x-1)(x^{2}+x+1)\) | 2 | 1,3 | 2 | |
| 4 | \((x-1)(x+1)(x^{2}+1)\) | 3 | 1,2,4 | 3 | |
| 5 | \((x-1)(x^{4}+x^{3}+x^{2}+x+1)\) | 2 | 1,5 | 2 | |
| 6 | \((x-1)(x+1)(x^{2}+x+1)(x^{2}-x+1)\) | 4 | 1,2,3,6 | 4 | |
| 7 | \((x-1)(x^{6}+x^{5}+x^{4}+x^{3}+x^{2}+x+1)\) | 2 | 1,7 | 2 | |
| 8 | \((x-1)(x+1)(x^{2}+1)(x^{4}+1)\) | 4 | 1,2,4,8 | 4 |
この表から分かるとおり、\(x^{n}-1\)を因数分解した場合の因子の個数と\(n\)の約数の個数は一致しています。これは、\(x^{n}-1=0\)の解を分類することにより示すことができます。以下\(x^{n}-1=0\)の解をいろいろな視点で眺めていきます。
代数的な視点から
\(x^{n}-1=0\)の解は\(n\)乗すると1となる数ですので、1の\(n\)乗根です。\(n\)次方程式の解は、複素数の中に(重根を含めて)\(n\)個ありますので(代数学の基本定理)、1の\(n\)乗根も\(n\)個あります。(なお、\(x^{n}-1=0\)が重根を持たないことは、ガウス平面上で考えることによって分かります。)
1の\(n\)乗根\(\zeta\)は、\(d\)乗してはじめて1になる場合を、原始\(d\)乗根といいます。\(d\)は\(n\)の約数になります。
1の原始\(d\)乗根は全部で\(\varphi(d)\)個あります。その\(\varphi(d)\)個の原始\(d\)乗根すべてを解とする多項式―\(\varphi(d)\)次式であり最高次数の係数が1であるもの―を\(\Phi_{d}(x)\)と記し円分多項式といいます。
円分多項式\(\Phi_{d}(x)\)は、次の性質があります。
1. 円分多項式\(\Phi_{d}(x)\)は整数係数多項式である。
2. 円分多項式\(\Phi_{d}(x)\)は整数係数多項式として既約である。
また、円分多項式の定義と1の\(n\)乗根の性質から
3. \(\displaystyle{x^{n}-1=\prod_{d|n}\Phi_{d}(x)}\)
が成立します。この式と1. 2.より\(x^{n}-1\)が\(n\)の約数個に因数分解できることが分かります。
\(\Phi_{n}(x)\)の\(n\)を日本語でどのように呼ぶのか悩ましいところです。当初、このブログでは\(n\)次円分多項式と呼んでいましたが、円分多項式の次数は\(\varphi(n)\)なので紛らわしいです。英語では\(n\)-th cyclotomic polynomialと言います。いわば、\(n\)番目の円分多項式というような意味で、次数(degree)と混同する心配はなさそうです。日本語ではなんと呼んだらよいんでしょうか?
円分体のガロア群
有理数体\(\mathbb{Q}\)に1の原始\(n\)乗根\(\zeta_{n}\)を添加した体\(\mathbb{Q}(\zeta_{n})\)を円分体といいます。円分体の\(\mathbb{Q}\)上の拡大次数は\(\varphi(n)\)です。下記は、円分体を特徴づける重要な性質です。
4. 円分体\(\mathbb{Q}(\zeta_{n})\)の有理数体\(\mathbb{Q}\)上のガロア群\(\text{Gal}(\mathbb{Q}(\zeta_{n})/\mathbb{Q})\)は\( (\mathbb{Z}/n\mathbb{Z})^{\times}\)と自然な同型がある
\[ \text{Gal}(\mathbb{Q}(\zeta_{n})/\mathbb{Q})\cong(\mathbb{Z}/n\mathbb{Z})^{\times}\]
5. したがって、円分体\(\mathbb{Q}(\zeta_{n})\)の有理数体\(\mathbb{Q}\)上巡回拡大(当然、アーベル拡大)である。
しかも、クロネッカー・ウェーバーの定理より、円分体は\(\mathbb{Q}\)上のアーベル拡大をすべて含む体となります。
(Kronecker–Weber Theorem)
\(K\)を\(\mathbb{Q}\)上の有限次アーベル拡大とする。このとき自然数\(n\)が存在し、\(K\)は円分体\(\mathbb{Q}(\zeta_{n})\)に含まれる。 \[ K\subset\mathbb{Q}(\zeta_{n})\]
この定理より、\(\mathbb{Q}\)上の有限次アーベル拡大\(K\)に対し、\(K\subset\mathbb{Q}(\zeta_{n})\)となる最少の自然数\(n\)が存在することが分かります。この最少の自然数\(n\)は類体論では重要な指標になります。
幾何的な視点から
1の\(n\)乗根をガウス平面上にプロットすると、単位円周上の等分点となります。これが円分多項式や円分体という用語の由来です。
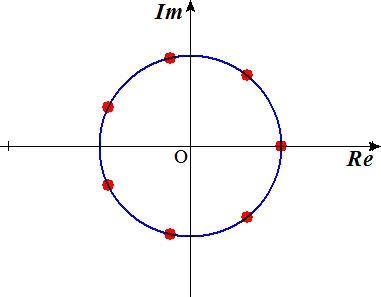
つまり、円の等分点を\(\mathbb{Q}\)に添加することにより、アーベル拡大が作れることになります。しかも、そのアーベル拡大は、\(\mathbb{Q}\)のアーベル拡大をすべて含むようなアーベル拡大なのです。
解析的な視点から
\(f(z)=\exp(zi)\)とするとオイラーの公式より\(f(z)\)は周期函数であることがわかります。
\[ f(z+2\pi)=\exp((z+2\pi)i)=\exp(zi)\exp(2\pi i)=\exp(zi)=f(z)\]
ですので周期\(2\pi\)であることが分かります。
また、\(f(z)\)は典型的な解析函数(無限回微分可能な複素函数。しかも、多項式などの代数的函数ではありません。)です。
そして、1の\(n\)乗根は\(f(z)\)を用いて
\[ f(0), f(\frac{2\pi}{n}), f(\frac{4\pi}{n}),\cdots, f(\frac{2(n-1)\pi}{n})\]
とあらわされます。つまり、1の\(n\)乗根は解析函数の特殊値として表すことができます。1の\(n\)乗根は代数的な数(多項式の解)ですが、これが解析函数の特殊値として表されることは興味深いことです。しかも、\(f(z)\)が周期函数であることは、楕円函数(二重周期函数)を考える重要な示唆となります。